Komplexa tal - Historia och nuvarande användning
Historien om komplexa tal
\sqrt{-1}=i är ett speciellt tal. i är grunden för det man kallar för komplexa tal. Komplexa tal har genom historien bemötts av förvirring och misstänksamhet av både elever och matematiker. Under en lång tid accepterade inte matematiker att det fanns komplexa tal men idag är de allmänt erkända och används mycket frekvent i modern matematik och fysik.
Historiskt ignorera man komplexa tal. Komplexa tal uppstår vanligtvis när man tar kvadratroten ur (eller 2n roten ur där n=1,2,3,4,5… ) ett negativt tal. Problematiken är att det finns inget reellt tal som multiplicerat med sig (jämnt antal gånger) blir negativt. Av den anledningen var matematiker skeptiska till dessa lösningar på ekvationer och bortsåg helt enkelt från det. Exempel på en sådana ekvationer är x^2+1=0 eller x^2+2x+2=0 . Den italienska matematikern Cardano (1501-1576) var den första att acceptera dess existens men samtidigt kallade han dem för ”värdelösa” och det var den synen man hade på komplexa tal under lång tid. Den store filosofen och matematikern Rene Decartes (1596-1650) var den som introducerade termen imaginära tal, eftersom han tänkte att dessa tal enbart var för tanken och inte för verkligheten. Termen imaginär ses ofta som ett dåligt ord för beskriva komplexa tal och nedan kommer du förstå varför.
Under 1700-talet vidareutvecklade Leonhard Euler den komplexa analysen. Man hade insett några år innan Euler att komplexa tal var väldigt användbara i beräknandet av trigonometriska funktioner. Det underlättade för beräkningar och man insåg dess praktiska nytta. Euler hittade sedan det som man kallar för Eulers formel: e^{i\beta}=cos(\beta)+isin(\beta) (e är basen för den naturliga logaritmen). Det här blev en revolution som resulterade i flera viktiga resultat från bland annat Caspar Wessel och Carl Friedrich Gauss. Man kunde visa komplexa tal går att uttryckas som en punkt i ett koordinatsystem där y-axeln är komplex och x-axeln reell. Man kunde sedan utnyttja Eulers identitet och visa att i går att använda för att beskriva vågrörelser på grund av dess koppling till trigonometri och dess egenskaper (se funktionen till höger).
Det fält inom matematiken som behandlar komplexa tal uppkom sedan och idag kallar vi den för komplex analys. Den utvecklades ytterligare med Bernhard Riemann som bland annat med hjälp av komplexa tal formulerade den kända Riemann-hypotesen, som verkar ha en koppling till primtal. Det ser alltså ut som att komplex analys går att sammanfoga med något som vi verkligen tycker är konkret nämligen primtal. Om du löser Riemann-hypotesen som du kan tjäna 1000000 dollar eftersom det ingår i milleniumproblemen.
Användningsområden idag
Idag används komplexa tal bland annat i ren matematik för att vidareutveckla den komplexa analysen men också inom andra fält inom matematiken och ingen matematiker ser idag på komplexa tal med skepsis.
Inom fysiken använder man komplexa tal hela tiden för att beskriva olika fysiska fenomen. Som tidigare stycke nämner är komplexa tal väldigt användbara för att kunna beskriva vågrörelser och när uträkningar blir för komplexa (hehe) vill man gärna hålla det enkelt och komplexa tal hjälper till med det. Vågrörelser dyker upp på flera ställen i fysiken: Analysen av strålning (till exempel ljus och radiovågor), analysen av hur en massa rör sig på en fjäder över tid, även inom ellära är komplexa tal användbara för att underlätta uträkningar.
Ett annat område inom fysiken där komplexa tal inte bara är ett användbart hjälpmedel utan måste användas för att förstå verkligheten är inom kvantfysiken. Kvantfysiken ses idag som en av de mest komplexa fälten inom fysiken och därför är det intressant att komplexa tal har en central roll i att kunna beskriva kvantfysiken matematiskt. Ett känt samband som beskriver centrala delar av kvantfysiken är Schrödingers ekvation (till höger). Schrödingers ekvation är en vågekvation som för att kunna representera verkligheten behöver talet i för att fungera. Man har kunnat verifiera med hjälp av experiment att sambandet i Schrödingers ekvation också stämmer. Det verkar alltså som inom fysiken behöver vi komplexa tal för att kunna beskriva hur världen fungerar. Därför är i ett fantastiskt tal som hjälper oss förstå och lösa några av de mest avancerade koncepten som vi kan finna.

Cardano (1501-1576)

En trigonometrisk funktion som är användbar för att beskriva vågrörelser
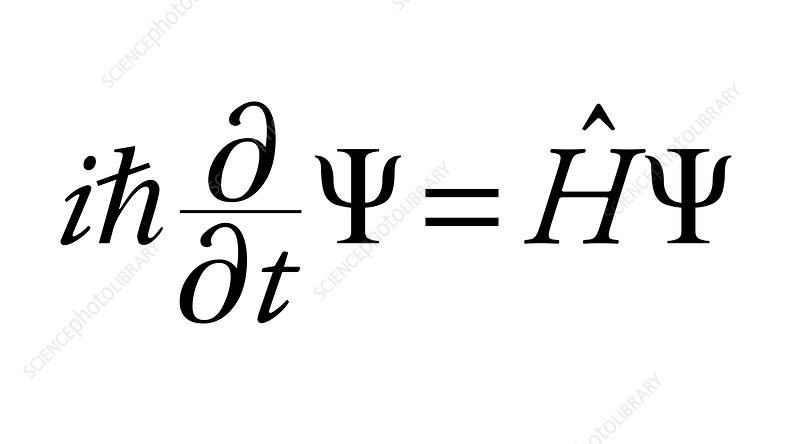
Schrödingers ekvation (notera i i vänsterledet)
